Site Inovação Tecnológica
Com informações do SINC
Escapar para o infinito
Construa uma "estrada magnética", um plano com um campo magnético, e você
será capaz de enviar partículas eletricamente carregadas para o infinito - elas
não vão parar nunca mais.
É o que garantem dois matemáticos da Universidade Complutense de Madri, na
Espanha.
Eles demonstraram matematicamente que as partículas podem "escapar para o
infinito".
"Se uma partícula 'escapa' para o infinito, isso significa duas coisas: que
ela nunca irá parar, e 'algo mais'," afirmou o professor Antonio Diaz-Cano, um
dos autores da teoria.
O "nunca irá parar" pode ser contornado, bastando aprisionar a partícula,
forçando-a a ficar eternamente fazendo círculos ao redor de um ponto, nunca
deixando um espaço fechado.
Entretanto, o "algo mais" significa que a partícula pode ir além desses
limites.
"Se imaginarmos uma superfície esférica com um grande raio, a partícula irá
cruzar a superfície tentando sair dela, não importando quão grande o raio possa
ser," escrevem os dois matemáticos.
Complexidade infinita
Uma das condições para escapar para o infinito é que o campo magnético seja
gerado por loops de corrente situados no mesmo plano de movimentação da
partícula.
A outra é que a partícula esteja em algum ponto do plano e a uma determinada
distância do campo magnético. E que seu movimento inicial seja paralelo a esse
plano.
"Nós não estamos dizendo que estas são as únicas condições para escapar para
o infinito, pode haver outras. Mas, nesse caso, nós confirmamos que o fenômeno
ocorre," garante Diaz-Cano.
De fato, os pesquisadores admitem que as condições ideais para que o fenômeno
ocorra são "um campo magnético e nada mais".
"Nós gostaríamos de ter sido capazes de testar algo mais geral, mas as
equações são muito mais complexas," completa.
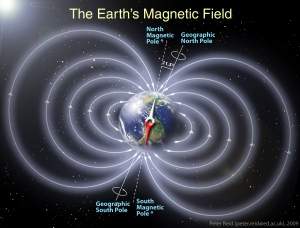 |
Os matemáticos não sabem se seria possível usar o campo magnético dos planetas para que as partículas escapem
para o infinito porque as equações para calcular isso são complexas demais.
[Imagem: Peter Reid]
|
Fusão nuclear e aceleradores de partículas
O problema é que a realidade tem suas próprias complexidades, como o atrito,
por exemplo.
Mas tampouco isso invalida a teoria e não impedirá que experimentalistas
comecem a testar o conceito muito rapidamente: na física do plasma, por
exemplo.
Eventualmente o fenômeno poderá ter impacto na área de fusão nuclear, onde os
físicos e engenheiros ainda não sabem exatamente como confinar o plasma dentro
de campos magnéticos.
Aceleradores com os do Grande Colisor de Hádrons (LHC) também usam campos
magnéticos para acelerar partículas.
Embora nesse caso não interesse aos físicos que as partículas escapem para o
infinito, mantê-las fazendo círculos ao infinito, adquirindo cada vez mais
velocidade, pode ser algo muito interessante.
 |
O projeto de fusão nuclear ITER já está em construção, embora os
engenheiros ainda não saibam como confinar o plasma em seu interior. [Imagem:
ITER Consortium]
|
O que é infinito?
Se você acha que a ideia de "escapar para o infinito" é estranha, você não
está sozinho. Afinal, o infinito não cobre tudo?
Não há uma resposta direta a essa pergunta. Afinal, a existência do infinito
tem sido debatida desde os tempos da Grécia antiga.
O fato de que o conceito pode levar a contradições lógicas desenvolveu o
chamado "medo do infinito", uma dúvida que tem-se mantido ao longo de
séculos.
No início do século XX, o matemático alemão David Hilbert (1862-1943) afirmou
que a matemática está "repleta de erros e absurdos, em grande parte devido ao
infinito".
Alguns especialistas acreditam que o debate não avançou muito desde a
antiguidade porque permanece aberta a discussão sobre o infinito atual ou real
(entendido como um todo) e o infinito potencial (que cresce ou se divide sem
fim) como Aristóteles considerava.
No entanto, é igualmente verdade que os matemáticos desenvolveram algumas
habilidades para lidar com o infinito.
A maior contribuição veio com o trabalho do russo Georg Cantor (1845-1918),
que introduziu diferentes tipos de infinito.
Por exemplo, um infinito enumerável - conjuntos de elementos que podem ser
contados com os números naturais - não é o mesmo que um infinito contínuo -
próprio de conjuntos como a reta.
Um dos grandes problemas da matemática durante o século XX foi a "hipótese do
contínuo", que consiste, essencialmente, em saber se há um "infinito
intermediário" entre os infinitos enumerável e contínuo.
Mas o problema do infinito não está restrito à matemática: há também um
infinito físico.
E infinito, fisicamente falando, pode ter dois significados, um prático e
outro cosmológico: por exemplo, o Universo é finito ou infinito?
Se tudo isso transcende a finitude do seu raciocínio, pelo menos agora você
pode se consolar: é possível escapar para o infinito.
Bibliografia:
Escape to infinity in the
presence of magnetic fields
Antonio Díaz-Cano Ocaña, F.
González-Gascón
Quarterly of Applied Mathematics
Vol.: 70 (1):
45-51
DOI: 10.1090/S0033-569X-2011-01248-4

Nenhum comentário:
Postar um comentário